"Ieder heeft zijn eigen voorkeur" hoor ik. Akkoord, dat is persoonlijk.
Aan de andere kant, de bedoeling van deze thread is toch om de verschillen duidelijk te maken, en dat gaat over feiten, daarover kunnen we helder zijn.
Veel is al helder nu.
Ik heb hier horen beweren dat deuvelen in plaatmaterial niet ideaal zou zijn maar ik begrijp het niet? Wat is daar niet ideaal aan? Waarom is dat beter met lamello's?
Heb je met lamello's niet het nadeel dat dit de plaat maar in 1 richting fixeert, en dat je in de lengte richting van de lamello moet klemmen of zo om het juist te krijgen?
Verder hoorde ik Pel vertellen dat domino 'sterker' is dan deuvel owv. groter lijmoppervlakte. Daar wil ik ook graag op reageren:
Geval 1: we maken de vereenvoudigde assumptie dat de sterkte in alle richtingen (puur) afhangt van de lijmsterkte
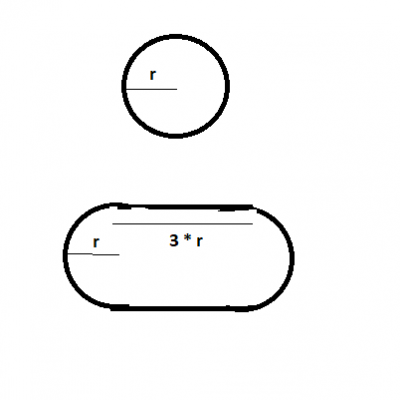
Laten we even samen rekenen. We vergelijken een deuvel en domino van dezelfde lengte en breedte.
Het lijmoppervlak is dan evenredig met de omtrek van de "cirkel" (deuvel) of "ovale rechthoek" bij de deuvel.
De omtrek van 2 deuvels (elke beweging schiet 2 deuvels): 2 * Pi * r per deuvel, dus 4 * Pi * r
Ik ken niet de exacte maat van een domino, maar laat ons stellen dat het 'rechthoekig' stukje 2 à 3 keer r is, dan is de omtrek:
2 * Pi * r (2x een half cirkeloppervlak, net als de deuvel) +
2 * x * r (rechthoekige stuk, waar x = 2 of 3). Laten we even 3,14 nemen, dan is dit gelijk aan Pi.
Totale omtrek: (2 * Pi + 2 * Pi ) * r = 4 * Pi * r. Dit oppervlak is dus min of meer gelijk aan 2 deuvels. Het maakt geen verschil. Ik heb waarschijnlijk overdreven met de breedte dus de domino heeft zelfs een klein nadeel.
Maar bon, dat is te simpel qua sterkte. Ten eerste: het contactoppervlak is niet volledig, want een deuvel is meestal geribbeld, en bij een domino, als je meerdere domino's per verbinding gebruikt, maak je ook gaten op de 'grotere' stand en heb je evenmin nog een volledig lijmoppervlak.
Ten tweede, de enige richting waar lijm van tel is, is in de trekrichting om ze uit elkaar te trekken. Met de prachtige domino of deuvelmachines zit alles zo strak dat in de andere richtingen de krachten puur mechanisch werken. In de richting van de breedte zijn beide systemen gelijk, in de richting van de lengte hangt het af hoever de deuvels/domino's uit elkaar zitten.
Dit allemaal gezegd zijnde, er is nog bijna niks van bekend, maar er komt dus een nieuwe deuvelaar aan, de DDF40. Ze zouden gewerkt hebben aan de ergonomie, het lijkt erop dat hij meer op de domino gaat lijken. Blijkbaar heeft de markt dus beslist dat de domino toch een beter systeem is, als ze bij Mafell dezelfde richting uitgaan. Foto's op de website van baptist:

Ik deuvel intussen lustig en tevreden voort met mijn "oude" DD40... ;-)
Aan de andere kant, de bedoeling van deze thread is toch om de verschillen duidelijk te maken, en dat gaat over feiten, daarover kunnen we helder zijn.
Veel is al helder nu.
Ik heb hier horen beweren dat deuvelen in plaatmaterial niet ideaal zou zijn maar ik begrijp het niet? Wat is daar niet ideaal aan? Waarom is dat beter met lamello's?
Heb je met lamello's niet het nadeel dat dit de plaat maar in 1 richting fixeert, en dat je in de lengte richting van de lamello moet klemmen of zo om het juist te krijgen?
Verder hoorde ik Pel vertellen dat domino 'sterker' is dan deuvel owv. groter lijmoppervlakte. Daar wil ik ook graag op reageren:
Geval 1: we maken de vereenvoudigde assumptie dat de sterkte in alle richtingen (puur) afhangt van de lijmsterkte

Laten we even samen rekenen. We vergelijken een deuvel en domino van dezelfde lengte en breedte.
Het lijmoppervlak is dan evenredig met de omtrek van de "cirkel" (deuvel) of "ovale rechthoek" bij de deuvel.
De omtrek van 2 deuvels (elke beweging schiet 2 deuvels): 2 * Pi * r per deuvel, dus 4 * Pi * r
Ik ken niet de exacte maat van een domino, maar laat ons stellen dat het 'rechthoekig' stukje 2 à 3 keer r is, dan is de omtrek:
2 * Pi * r (2x een half cirkeloppervlak, net als de deuvel) +
2 * x * r (rechthoekige stuk, waar x = 2 of 3). Laten we even 3,14 nemen, dan is dit gelijk aan Pi.
Totale omtrek: (2 * Pi + 2 * Pi ) * r = 4 * Pi * r. Dit oppervlak is dus min of meer gelijk aan 2 deuvels. Het maakt geen verschil. Ik heb waarschijnlijk overdreven met de breedte dus de domino heeft zelfs een klein nadeel.
Maar bon, dat is te simpel qua sterkte. Ten eerste: het contactoppervlak is niet volledig, want een deuvel is meestal geribbeld, en bij een domino, als je meerdere domino's per verbinding gebruikt, maak je ook gaten op de 'grotere' stand en heb je evenmin nog een volledig lijmoppervlak.
Ten tweede, de enige richting waar lijm van tel is, is in de trekrichting om ze uit elkaar te trekken. Met de prachtige domino of deuvelmachines zit alles zo strak dat in de andere richtingen de krachten puur mechanisch werken. In de richting van de breedte zijn beide systemen gelijk, in de richting van de lengte hangt het af hoever de deuvels/domino's uit elkaar zitten.
Dit allemaal gezegd zijnde, er is nog bijna niks van bekend, maar er komt dus een nieuwe deuvelaar aan, de DDF40. Ze zouden gewerkt hebben aan de ergonomie, het lijkt erop dat hij meer op de domino gaat lijken. Blijkbaar heeft de markt dus beslist dat de domino toch een beter systeem is, als ze bij Mafell dezelfde richting uitgaan. Foto's op de website van baptist:

Ik deuvel intussen lustig en tevreden voort met mijn "oude" DD40... ;-)

