piramidedak
- Onderwerp starter eightball
- Startdatum
Je gebruikt een verouderde webbrowser. Het kan mogelijk deze of andere websites niet correct weergeven.
Het is raadzaam om je webbrowser te upgraden of een alternatieve webbrowser te gebruiken.
Het is raadzaam om je webbrowser te upgraden of een alternatieve webbrowser te gebruiken.
De gemakkelijkste manier is om het even uit te tekenen, dat mag op schaal.
Teken het grondvlak en teken er een diagonaal in, op het midden van de diagonaal teken je een loodrechte, de lengte van deze lijn word de hoogte van de piramide.
Verbind de twee eindpunten van de diagonaal met de top van de loodrechte, het resultaat is een dubbele driehoek.
Die tekening bevat alle hoeken en afmetingen die je nodig hebt om de piramide te bouwen
Zo simpel kan het leven zijn.
Mvg,
André
Teken het grondvlak en teken er een diagonaal in, op het midden van de diagonaal teken je een loodrechte, de lengte van deze lijn word de hoogte van de piramide.
Verbind de twee eindpunten van de diagonaal met de top van de loodrechte, het resultaat is een dubbele driehoek.
Die tekening bevat alle hoeken en afmetingen die je nodig hebt om de piramide te bouwen
Zo simpel kan het leven zijn.
Mvg,
André
Verstek piramide berekenen
Bij het maken van een piramide loop ik ook tegen de moeilijkheid op dat ik de verstekhoek waarin ik de lange zijden moet zagen niet berekend krijg. Ik heb nu met trial and error de zijden bijna pas verstek gemaakt ( mijn piramide werd steeds kleiner ;-) ) maar vraag me af hoek ik dit kan berekenen. Ik heb alle oude kennis van sinussen, cosinussen en tangens weer opgediept, maar tevergeefs.
Ik vond op internet deze berekeningssite, maar de hier aangegeven hoek ("snedehoek") klopte voor mij ook niet.
Ook met onderstaande uitleg kom ik er als alpha niet uit. Heeft iemand wellicht hiervoor een rekenvoorbeeld?
Alvast dank.
Bij het maken van een piramide loop ik ook tegen de moeilijkheid op dat ik de verstekhoek waarin ik de lange zijden moet zagen niet berekend krijg. Ik heb nu met trial and error de zijden bijna pas verstek gemaakt ( mijn piramide werd steeds kleiner ;-) ) maar vraag me af hoek ik dit kan berekenen. Ik heb alle oude kennis van sinussen, cosinussen en tangens weer opgediept, maar tevergeefs.
Ik vond op internet deze berekeningssite, maar de hier aangegeven hoek ("snedehoek") klopte voor mij ook niet.
Ook met onderstaande uitleg kom ik er als alpha niet uit. Heeft iemand wellicht hiervoor een rekenvoorbeeld?
Alvast dank.
De gemakkelijkste manier is om het even uit te tekenen, dat mag op schaal.
Teken het grondvlak en teken er een diagonaal in, op het midden van de diagonaal teken je een loodrechte, de lengte van deze lijn word de hoogte van de piramide.
Verbind de twee eindpunten van de diagonaal met de top van de loodrechte, het resultaat is een dubbele driehoek.
Die tekening bevat alle hoeken en afmetingen die je nodig hebt om de piramide te bouwen
Zo simpel kan het leven zijn.
Mvg,
André
Ik heb twee jaar geleden parket gelegd in een huis met een hoek in. Lang mijn kop gebroken over een manier om de helft van die
Dat op schaal tekenen zoals voorgesteld is een goede methode als je heel precies kan tekenen. Je vergroot de teken- en meetfouten terug mee uit. Misschien kan je een vergelijkbare techniek toepassen.
Span een touw (goed strak) van de basis van je piramide naar je top (als die er al staan natuurlijk). Leg dan een blad (A4'tje volstaat) met één kant op de basis en vouw het over je touwtje. Nu heb je de exacte hoek die je moet hebben. Vouw je blad dat nu de hoek vertegenwoordigt zo op dat de benen van de hoek op elkaar liggen en je hebt de hoek van je verstek. Als je benen en basis in verstek wil kan je dat zo doen. Als je enkel de benen schuin afzaagt kan dat ook zo, maar dan moet je anders vouwen.
Dat op schaal tekenen zoals voorgesteld is een goede methode als je heel precies kan tekenen. Je vergroot de teken- en meetfouten terug mee uit. Misschien kan je een vergelijkbare techniek toepassen.
Span een touw (goed strak) van de basis van je piramide naar je top (als die er al staan natuurlijk). Leg dan een blad (A4'tje volstaat) met één kant op de basis en vouw het over je touwtje. Nu heb je de exacte hoek die je moet hebben. Vouw je blad dat nu de hoek vertegenwoordigt zo op dat de benen van de hoek op elkaar liggen en je hebt de hoek van je verstek. Als je benen en basis in verstek wil kan je dat zo doen. Als je enkel de benen schuin afzaagt kan dat ook zo, maar dan moet je anders vouwen.
Heeft iemand wellicht hiervoor een rekenvoorbeeld?
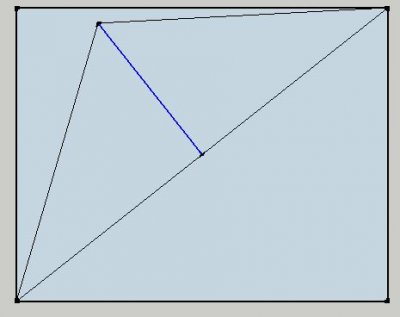
André zijn uitleg in tekening: de diagonaal, de hoogte als loodrechte en de dubbele driehoek. Van daaruit kan je de hoeken en lengtes overnemen.
Ik was laatst aan het kijken hoe Amerikaanse schrijnwerkers het doen, ze hebben ondermeer de hoeken voor vierkante piramides reeds aangegeven op hun speed-square en de nodige lengtes als tabellen op hun framing square.
@Andre. Nu heb je lengte van de zijden. En de hoek van 2 tegenoverstaande zijden. Maar zoals je algemeen bekend is, is dat bij een dubbelverstek de zijden (uitgaande van 4 zijden) onderling niet onder een hoek van 45 graden staan. Hoe bereken jij deze hoek dan?
Renault: volgens mij berekent Andre weinig in dit geval. Op schaal uittekenen wil zeggen dat je de hoeken met een zweihaak gewoon kan overnemen van de tekening? Enfin dat veronderstel ik toch uit zijn uitleg.
Ik zal de hoek niet uitrekenen maar je kan het terugrekenen met de stelling van Pythagoras. zie online calculators.
de basis vierkant is bijvoorbeeld 5 meter, de hoogte van de pyramide is 3 meter
dan is A 250, B is 300 uitkomst berekening = C 390,5 (c is de lengte van je dakvlak en a is halve lengte van een zijde van je vierkant)
nu reken je uit wat de lengte van de schuine hoek van je dak is.
in dit geval;
A = 250, B = 390,5 uitkomst C = 463,67 (A = halve lengte vierkant, B = lengte dakvlak en C is schuine lengte dakvlak)
stel je gebruikt delen/schroten van een werkende breedte van 20 cm lengte 5 meter, in de eerste berekening was de lengte van het dak 390,5 gedeeld door 20 cm is 19,52 stuks delen/schroten
C was 463,67 gedeeld door 19,52 dan is de lengte van je schuine zaagsnede 23,75 cm, deze zet je uit op je deel/schroot dan zie dat er een puntje van 12,6 cm afgaat x 2 = volgende deel korter (belangrijk voor je zaaglijst)
Leg je gradenboog eroverheen dan zie je dat je hoek ongeveer 57,5 graden (of 32,5) is, je aanslag hierop instellen en de zaag kantelen op 45 graden en zagen maar.
even jezelf controleren? 19,5 delen x 25,4cm afval is 495 cm = goed genoeg voor een dak. (dat laatste halve deeltje bovenaan is je passtuk)
Ik hoop dat ik het begrijpelijk uitleg.
de basis vierkant is bijvoorbeeld 5 meter, de hoogte van de pyramide is 3 meter
dan is A 250, B is 300 uitkomst berekening = C 390,5 (c is de lengte van je dakvlak en a is halve lengte van een zijde van je vierkant)
nu reken je uit wat de lengte van de schuine hoek van je dak is.
in dit geval;
A = 250, B = 390,5 uitkomst C = 463,67 (A = halve lengte vierkant, B = lengte dakvlak en C is schuine lengte dakvlak)
stel je gebruikt delen/schroten van een werkende breedte van 20 cm lengte 5 meter, in de eerste berekening was de lengte van het dak 390,5 gedeeld door 20 cm is 19,52 stuks delen/schroten
C was 463,67 gedeeld door 19,52 dan is de lengte van je schuine zaagsnede 23,75 cm, deze zet je uit op je deel/schroot dan zie dat er een puntje van 12,6 cm afgaat x 2 = volgende deel korter (belangrijk voor je zaaglijst)
Leg je gradenboog eroverheen dan zie je dat je hoek ongeveer 57,5 graden (of 32,5) is, je aanslag hierop instellen en de zaag kantelen op 45 graden en zagen maar.
even jezelf controleren? 19,5 delen x 25,4cm afval is 495 cm = goed genoeg voor een dak. (dat laatste halve deeltje bovenaan is je passtuk)
Ik hoop dat ik het begrijpelijk uitleg.
Laatst bewerkt:
Toch is dit niet zo moeilijk te berekenen...als ik de vraag goed begrijp tenminste.
Voorbeeld:
Uitgangspunten:
Grondvlak:
lengte x breedte = 20 x 20
Hoogte gewenste piramide = 8
Berekening:
Diagonaal grondvlak= √ (20^2 + 20^2)=√800=28,28
Snedehoek = inverse tan (hoogte/0,5 x diagonaal) = inverse tan (8/14,14) = inverse tan 0,566 = 29,5 graden.
Controleer maar met de site. Als ik meer moet uitrekenen dan wordt dat morgen.
Rob
Voorbeeld:
Uitgangspunten:
Grondvlak:
lengte x breedte = 20 x 20
Hoogte gewenste piramide = 8
Berekening:
Diagonaal grondvlak= √ (20^2 + 20^2)=√800=28,28
Snedehoek = inverse tan (hoogte/0,5 x diagonaal) = inverse tan (8/14,14) = inverse tan 0,566 = 29,5 graden.
Controleer maar met de site. Als ik meer moet uitrekenen dan wordt dat morgen.
Rob
@Andre. Nu heb je lengte van de zijden. En de hoek van 2 tegenoverstaande zijden. Maar zoals je algemeen bekend is, is dat bij een dubbelverstek de zijden (uitgaande van 4 zijden) onderling niet onder een hoek van 45 graden staan. Hoe bereken jij deze hoek dan?
De verstekzaag kantelen naar de halve hoeken tussen de diagonalen? Of zie ik het te simpel, de balken zijn onder een hoek maar niet gekanteld. De lengte wordt dan op een middenlijn genomen niet op een kant.
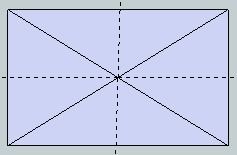
De zijden staan niet onder een hoek van 45° met elkaar, maar de zaaglijn staat wel onder 45° met het schuine (buiten)vlak. Bekijk maar een vlak loodrecht op de ribben: de zijvlakken van de piramide maken daar een rechte hoek, en als je die in tweeën deelt krijg je 2x 45°. Dat vlak staat ook loodrecht op het schuine vlak van de piramide, dus de hoek die de zaaglijn maakt met dat vlak is 90°-45° is ook 45°.
Ik heb er ook even mee zitten worstelen in de voorstelling. Je hebt de neiging om de hoek van de gezaagde kant tov. de basis te bekijken of tov. de hoogte. Maar dat moet je niet hebben, je moet de hoek tov. het schuine vlak hebben. Die is gewoon 45°.
Ik heb er ook even mee zitten worstelen in de voorstelling. Je hebt de neiging om de hoek van de gezaagde kant tov. de basis te bekijken of tov. de hoogte. Maar dat moet je niet hebben, je moet de hoek tov. het schuine vlak hebben. Die is gewoon 45°.
Hallo,
Een timmerman maakt van een dak met deze vorm een uitslag om de vorm en afmeting van het dakvlakken en de hoekkeperbalk te bepalen alsmede de afschuining van de hoekkeperbalk. (hiermee kun je ook de zaagschuinte van de schuine zijden bepalen)
Daar komt geen rekenwerk, maar tekenwerk bij kijken.
Om dit in woorden uit te leggen is bijna niet mogelijk daarom heb ik dit uitgetekend, maar mijn computerkennis is niet zo groot dat mij dit zelfstandig lukt en kan ook nergens vinden hoe dit moet.
Vanavond komt hulp zodat ik het dan misschien gepost krijg .
Jan.
Een timmerman maakt van een dak met deze vorm een uitslag om de vorm en afmeting van het dakvlakken en de hoekkeperbalk te bepalen alsmede de afschuining van de hoekkeperbalk. (hiermee kun je ook de zaagschuinte van de schuine zijden bepalen)
Daar komt geen rekenwerk, maar tekenwerk bij kijken.
Om dit in woorden uit te leggen is bijna niet mogelijk daarom heb ik dit uitgetekend, maar mijn computerkennis is niet zo groot dat mij dit zelfstandig lukt en kan ook nergens vinden hoe dit moet.
Vanavond komt hulp zodat ik het dan misschien gepost krijg .
Jan.
@Andre. Nu heb je lengte van de zijden. En de hoek van 2 tegenoverstaande zijden. Maar zoals je algemeen bekend is, is dat bij een dubbelverstek de zijden (uitgaande van 4 zijden) onderling niet onder een hoek van 45 graden staan. Hoe bereken jij deze hoek dan?
Sorry voor de onduidelijkheid, ging er van uit dat er sprake was van een daktimmer, daar vind je alle noodzakelijke hoeken voor op de tekening.
Die bewuste hoek bereken ik niet
Hoe ga ik te werk? Stel je gaat een pyramide bouwen in plaatmateriaal van 10mm dikte. Ik zaag 4 stukken plaat (iets te ruim) waar de zijden uit gaan gezaagd worden. Bij twee van deze platen zaag ik al 1 kant voorlopig op schuinte, deze hoek kan je overnemen van de tekening, de kopse kant is hier nog 90°. Zet de 2 stukken plaat met de schuin gezaagde zijden tegen elkaar en laat ze onderaan tegen het grondvlak raken, zo ben je zeker dat ze een hoek van 90° maken. De 2 platen leunen nu voorover en de gemeenschappelijke schuin gezaagde randen raken elkaar nu over de volledige lengte, maar op de dikte gezien staan ze aan de buitenkant open; wat logisch is natuurlijk.
Meet deze opening, stel dat je hier een waarde meet van 9mm, dan wil dat zeggen dat de schuine zijden 4,5mm onderuit moeten gezaagd worden om eens op hun plaats mooi te sluiten. Dit wil ook zeggen dat de vier driehoeken die de zijden gaan vormen 2 x 4,5mm breder moeten gezaagd worden, anders word de pyramide te klein.
Bij grote pyramides zoek je die hoeken op met twee kleinere stukken afvalplaat. Stel dat de riblengte 3m moet worden, dan kan je de binnenhoek al bepalen met 2 stukken plaat van 30 cm breedte, al wat je moet doen is aan die twee stukken afval al één schuinte te zagen, deze kan je daarna eveneens tegen het grondvlak plaatsen, de 2 stukken laten voorover hellen tot de gemeenschappelijke schuin gezaagde zijden tegen elkaar komen te rusten, en daarna de opening langs buiten te meten. Daarna eveneens de uitkomst delen door 2, en op deze gevonden waarde de platen onderuit zagen. Past gegarandeerd altijd.
Ik hoop dat één en ander duidelijk is? 'T is altijd lastig te omschrijven, het "doen" is heel wat makkelijker en sneller
Mvg,
André
Hallo,
De tekening is getekend voor een vierkant object met het hoogste punt (T)in het midden, maar is toepasbaar voor elke (niet gebogen) 3 tot meerzijdige vorm van object waarbij het hoogste punt niet in het midden hoeft te liggen.
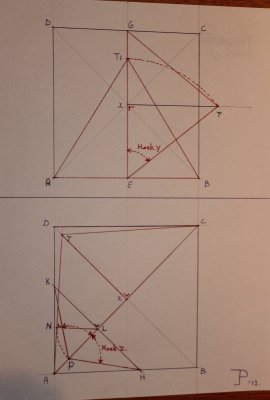
Met behulp van bijgevoegde tekening moet mijn uitleg zeker lukken.
Vierkant ABCD is de basis (de zoldervloer) en X is de loodlijn uit de top.
In de bovenste tekening bepalen we de vorm en afmeting van het dakvlak (de 4 vlakken zijn hier even groot)
Zet vanuit X de loodrechte hoogtemaat van het dak uit X-T haaks op lijn E-G.
Cirkel vanuit E de maat E-T om naar de lijn E-G is punt T1
Driehoek ABT1 is de vorm (en als je op ware grootte hebt getekend) en de afmeting van het dakvlak.
Hoek Y is de hoek waarmee de onderkant (lijn A-B) gezaagd moet worden.
Om de schuinte van de raakvlakken van de dakpleten te bepalen hebben we de onderste tekening nodig.
Ik heb 2 tekeningen gemaakt voor de duidelijkheid maar dit is niet echt nodig.
Wat wel nodig is dat je zuiver tekent en zeer nauwkeurig je maten afmeet.
Teken op de lijn A-C in X haaks op A-C de loodrechte hoogtemaat van het dak uit X-T .dit is punt T .
Trek de lijn A-T .
Teken ergens de lijn H-K haaks op lijn A-C . op lijn A C vind je nu punt L .
Teken vanuit punt L een lijn die haaks op lijn A-T staat is punt N .
Cirkel uit punt L de lijn L-N om naar lijn A-C is punt P .
Teken lijn H-P.
De hoek tussen lijn A-C en lijn H-P (hoek Z0 is de hoek wwarop de dakplaten aan de zijkant afgezaagd moeten worden.
Heb je nog verdere vragen of is het niet duidelijk dan hoor ik dit graag.
Veel succes .
Jan.
De tekening is getekend voor een vierkant object met het hoogste punt (T)in het midden, maar is toepasbaar voor elke (niet gebogen) 3 tot meerzijdige vorm van object waarbij het hoogste punt niet in het midden hoeft te liggen.

Met behulp van bijgevoegde tekening moet mijn uitleg zeker lukken.
Vierkant ABCD is de basis (de zoldervloer) en X is de loodlijn uit de top.
In de bovenste tekening bepalen we de vorm en afmeting van het dakvlak (de 4 vlakken zijn hier even groot)
Zet vanuit X de loodrechte hoogtemaat van het dak uit X-T haaks op lijn E-G.
Cirkel vanuit E de maat E-T om naar de lijn E-G is punt T1
Driehoek ABT1 is de vorm (en als je op ware grootte hebt getekend) en de afmeting van het dakvlak.
Hoek Y is de hoek waarmee de onderkant (lijn A-B) gezaagd moet worden.
Om de schuinte van de raakvlakken van de dakpleten te bepalen hebben we de onderste tekening nodig.
Ik heb 2 tekeningen gemaakt voor de duidelijkheid maar dit is niet echt nodig.
Wat wel nodig is dat je zuiver tekent en zeer nauwkeurig je maten afmeet.
Teken op de lijn A-C in X haaks op A-C de loodrechte hoogtemaat van het dak uit X-T .dit is punt T .
Trek de lijn A-T .
Teken ergens de lijn H-K haaks op lijn A-C . op lijn A C vind je nu punt L .
Teken vanuit punt L een lijn die haaks op lijn A-T staat is punt N .
Cirkel uit punt L de lijn L-N om naar lijn A-C is punt P .
Teken lijn H-P.
De hoek tussen lijn A-C en lijn H-P (hoek Z0 is de hoek wwarop de dakplaten aan de zijkant afgezaagd moeten worden.
Heb je nog verdere vragen of is het niet duidelijk dan hoor ik dit graag.
Veel succes .
Jan.
Duidelijke uitleg Jan, bedankt. Twee vraagjes over de tweede constructie: de hoek die je bepaalt, is dat de hoek van de horizontale zaagsnede? En als HK 'ergens' op AC mag liggen zou je daarvoor ook BD kunnen nemen. Is er een reden dat je dat niet doet?
Wow Jan, het zou zo inderdaad te berekenen moeten zijn, klinkt logisch, maar moet er wel even voor gaan zitten. Ik ga vanavond je voorbeeld op mijn casus loslaten voor de exacte berekening. In eerste instantie heb ik de trial and error methode toegepast maar meten over zoveel schijven is nooit zo precies als berekenen. Dank voor de uitleg.
Voor diegenen die het rekenen of tekenen niet zien zitten, hierbij een kant en klaar progje. Enkel twee gegevens invullen en na een druk op de knop rollen alle relevante hoeken eruit.
Je kan het resultaat nog uitprinten ook
Kl****, kan het ding niet als bijlage uploaden, het is een .xls extensie. Iemand een oplossing voor dit probleem?
Mvg,
André
Je kan het resultaat nog uitprinten ook
Kl****, kan het ding niet als bijlage uploaden, het is een .xls extensie. Iemand een oplossing voor dit probleem?
Mvg,
André
Hallo André,
Ik heb een beetje zitten testen.
Er zijn twee mogelijkheden:
1. Je zet het XLS bestand om in een gecomprimeerd bestand, zoals zip of rar. Dat formaat wordt door dit forum aanvaard. De mensen die het downloaden moeten het dan "uitpakken" naar het oorspronkelijke xls formaat.( gebeurt automatisch of met één klik)
Er zijn veel programmaatjes om iets te "zippen". Ik veronderstel dat je met Windows werkt. Omdat ik al jaren alleen nog Linux gebruik weet ik niet meer wat het beste progje voor Windows is.
2. Je upload je bestand naar een file-sharing site (bijvoorbeeld Rapidshare) en zet hier de link naar die site, zodat forumleden het programma vanaf die site kunnen downloaden.
MVG,
Bert
Ik heb een beetje zitten testen.
Er zijn twee mogelijkheden:
1. Je zet het XLS bestand om in een gecomprimeerd bestand, zoals zip of rar. Dat formaat wordt door dit forum aanvaard. De mensen die het downloaden moeten het dan "uitpakken" naar het oorspronkelijke xls formaat.( gebeurt automatisch of met één klik)
Er zijn veel programmaatjes om iets te "zippen". Ik veronderstel dat je met Windows werkt. Omdat ik al jaren alleen nog Linux gebruik weet ik niet meer wat het beste progje voor Windows is.
2. Je upload je bestand naar een file-sharing site (bijvoorbeeld Rapidshare) en zet hier de link naar die site, zodat forumleden het programma vanaf die site kunnen downloaden.
MVG,
Bert
Bijlagen
Duidelijke uitleg Jan, bedankt. Twee vraagjes over de tweede constructie: de hoek die je bepaalt, is dat de hoek van de horizontale zaagsnede? En als HK 'ergens' op AC mag liggen zou je daarvoor ook BD kunnen nemen. Is er een reden dat je dat niet doet?
De hoek Z is de hoek die aan de zijde A-T1 en B-T1 gezaagd moet worden.
Hoek Z is alleen 45 graden als de zijden recht op staan, bij een hellend dakvlak is de te zagen hoek altijd groter dan 45 graden.
HK mag op BD liggen maar als ik dat als voorbeeld had genomen was de tekening er niet duidelijker op geworden.
Jan.
Laatst bewerkt:
Deze plek is voor toekomstige tekst. Door nu alvast deze kolom te activeren blijft de kolommen structuur ongewijzigd en de lezerservaring hetzelfde als er hier content geplaatst gaat worden.
Hier kan straks ook info geplaatst worden.

