Ik denk dat ik er wel uit ben ondertussen

(Hoezo, nachtje wakker gelegen!?)
Het ~echte~ antwoord is ruimtemeetkunde: de hoek tussen twee dakdelen bepalen (a.d.h.v. hun normaallijnen), en deze hoek dan in twee delen omdat je van beide dakdelen precies de helft wil afhalen. Als de ruimtehoek bvb 150* is, heb je dus 180*-150*=30* te verdelen, of 15* per dakdeel. Je mitert dus onder 90-15=75*. (Doe even alsof die sterretjes ‘graden’ zijn en dan moet ik niet op een qwerty op zoek naar dat hoge bolletje).
Maar bon, ruimtemeetkunde is Chinees voor mij (geworden). Voor alle duidelijkheid: ik spreek geen Chinees. Dus alternatieven zoeken...
De truc zit ‘m in de top. Alle acht
pizzapunten/dakdelen hebben
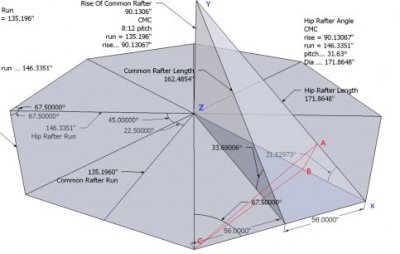
twee gemeenschappelijke punten in de top: eentje op de bovenkant van een dakdeel (t.t.z. de eigenlijke top vh dak uiteraard), maar ook eentje op de onderkant van het dakdeel (de ‘binnenste top’ als het ware). Als we nu een loodrecht vlak definiëren door dat ~onderste~ raakpunt, loodrecht op het dakdeel, dan vormt de snede van dat vlak met het dakdeel een gelijkbenige driehoek, met het onderste raakpunt als top van deze gelijkbenige driehoek, en met de twee andere hoeken op de buitenste ribben van het dakdeel. Deze driehoek is perfect te berekenen a.d.h.v. de dikte van het dakdeel (dit is namelijk de hoogte vd gelijkbenige driehoek) en de hellinghoek vh dakdeel (dewelke de gelijkbenige hoek bepaalt), en dit met gewone driehoeksmeetkunde (hoezo, 20 jaar geleden!?), of desnoods zelfs met een projectietekening (hoezo, 25 jaar geleden!?).
En nu komt de clou: de helling van de zijden van de gelijkbenige driehoek – die we net hebben berekend – is uiteraard de helling van de zijden van het dakdeel (want we hadden een loodrechte doorsnede gemaakt), en dus ook meteen je miterhoek.
Klaar.
Euh, nu nog even de tekening en de berekening.
Straks.
Als er niks op TV is.
En Youtube plat ligt.
En de kinderen niet om pap schreeuwen.