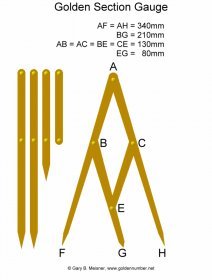
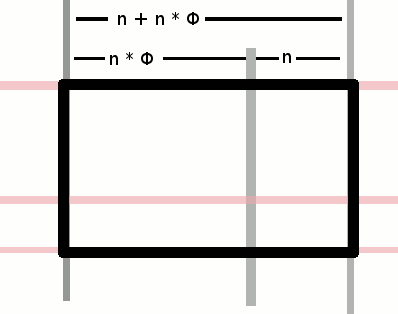
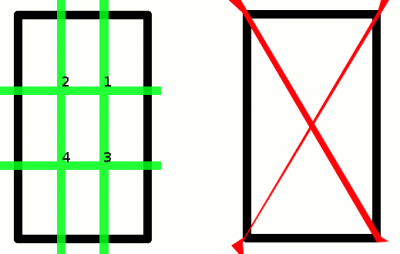
De gulden snede duikt op allerlei onverwachte plaatsen op, zoals in de architectuur, bij de lengte van je vingerkootjes, bij een bloemkool, de vorm van een boom.
De gulden snede is een stukje eeuwenoude raadselachtige wiskunde. De gulden snede of ‘Divina Proportia’ (goddelijke proportie) kort men af met de Griekse letter Φ (spreek uit: ‘Fie’). Φ heeft niets met π te maken. π ken je wel van de wiskundeles. Het drukt de verhouding van de diameter van een cirkel uit in relatie tot de omtrek en heeft als waarde 3,14. Φ geeft een verhouding van lijnstukken aan – vandaar de Engelse naam: The Golden Ratio.
Sommige onderzoekers denken dat de beroemde piramides van de oude Egyptenaren zijn gebouwd op basis van het getal Φ.
De Griekse wijsgeer Euclides beschreef als eerste het getal Φ, maar men gebruikte de gulden snede waarschijnlijk al eerder. De oude Egyptenaren bouwden hun piramides op basis van de gulden snede. Ook in het Parthenon, een tempel ter ere van de godin van welvaart en vrede Athena, kun je Φ terugvinden. Φ is ook op andere plaatsen te ontdekken: bijvoorbeeld in de verhouding tussen de lengte van het middelste botje in je vinger tot het langste botje en het kortste botje. Ook in het hartslagpatroon – zichtbaar gemaakt op een ECG – is tussen de hartslagen de verhouding van Φ terug te vinden. In de vroege middeleeuwen bedacht Fibonacci het antwoord op de vraag waarom deze verhouding zo vaak terug te vinden is.
In 1202 publiceerde Leonardo Fibonacci een bijzondere rij getallen: elk getal van de rij (behalve de eerste twee) is gelijk aan de som van de twee voorgaande getallen. Dat levert de volgende rij getallen op: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, enzovoorts. De Fibonacci-reeks zit vol met eigenaardigheden, zoals elke optelsom van tien opeenvolgende getallen uit de reeks is deelbaar door elf (probeer maar eens). Om de zestig getallen herhaalt het laatste cijfer, bijvoorbeeld het tweede getal is 1, het tweeënzestigste getal in de reeks eindigt op een 1 (….4052739537881), het 122ste getal in de reeks eindigt op een ….. 1 (…..14028366653498915298923761), etcetera.
De Fibonacci-reeks vormt de rekenkundige basis voor de gulden snede. Dit is in 1611 ontdekt door de beroemde astronoom Johannes Kepler. Als je een getal uit de Fibannaci-reeks deelt door zijn voorganger uit de reeks, dan benadert de breuk het gulden-snede-getal Φ. In de tabel staan enkele getallen uit de Fibonacci-reeks gedeeld door het voorgaande getal, afgerond op vijf decimalen.
De Fibonnanci-reeks komt in de natuur op allerlei onverwachte plaatsen voor. Als je bijvoorbeeld goed kijk naar de verdeling van de zonnebloemzaden in een zonnebloem, kun je spiralen zien waarvan sommige met de klok meedraaien en sommige tegen de klok in lopen. De grootte van de zonnebloem bepaalt het aantal spiralen. Meestal tel je 34 spiralen die de ene kant op wijzen en (je raadt het al) 55 die de andere kant op wijzen. Bestudeer eens een bloemkool van de bovenkant. Als je goed kijkt, kun je hier ook een spiralenpatroon zien (meestal 5 met de klok mee en 8 tegen de klok in). Ook de rangschikking van blaadjes rond de stengel van een plant volgt vaak de beroemde reeks. De blaadjes zitten niet allemaal aan dezelfde kant van een stengel, maar staan spiraalsgewijs om de stengel. Het aantal blaadjes per omloop volgt de Fibonacci-reeks, bijvoorbeeld per omwenteling om de stam staan twee blaadjes (1/2) of acht blaadjes per drie omwentelingen.

Wonderlijke spiraal
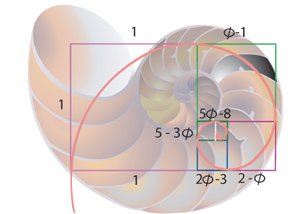
Deze logaritmische spiraal komt in de natuur veelvuldig voor. Deze wonderlijke spiraal (Spiralis Mirabilis) wordt ook wel de Spiraal van Archimedes genoemd. Archimedes was helemaal gebiologeerd door spiralen en schreef er zelfs een compleet boek over.Veel slakkenhuizen zijn volgens dit patroon opgebouwd. Ook de hoorns van bijvoorbeeld een ram volgen dit patroon, maar ook sterrenstelsels. Uit figuur 5 blijkt dat de Spiralis Mirabilis rechtstreeks uit Φ is afgeleid. Kunstenaars maken veelvuldig van de spiraal gebruik. In de krullen van Leda, op het schilderij Leda en de zwaan van Leonardo da Vinci kun je ook de Spira mirabilis vinden.
Knappe vriendin
Waarom stemt het ene schilderij meer met de werkelijkheid overeen dan een ander schilderij? Volgens Pacioli (1445- 1517) – een Italiaanse wiskundige kloosterling – komt dat doordat de schilder de wetten van de wiskunde gehoorzaamt. Diepte in een schilderij, de verdeling van ruimtelijke vlakken over het linnen, liggen volgens Pacioli allemaal vast in wiskundige verhoudingen zoals Φ. Hij schreef drie boeken (bekend onder de naam ‘De Divina Proportione’) waarin hij de schilderkunst tot wiskundige figuren en vergelijkingen probeerde terug te brengen. Ook schilders uit recentere tijden zoals Mondriaan gebruikten bewust dan wel onbewust de gulden snede.
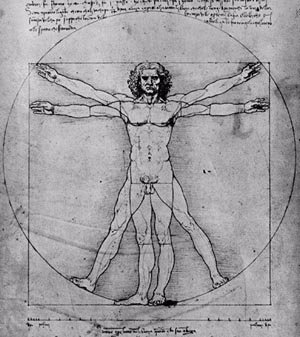
Niet alleen in de kunst kom je Φ tegen, ook menselijke schoonheid volgt de wetten van de gulden snede. In het menselijke gezicht vind je allerlei verhoudingen die de gulden snede benaderen. Bijvoorbeeld de verhouding van de lengte van je neus tot de breedte. Of de afstand tussen je ogen tot de totale breedte van je gezicht. Misschien verklaart het aantal gulden sneden die in het gezicht voorkomen, of iemand knap is of niet. Dus als je wilt weten of je een knappe vriend of vriendin aan de haak hebt geslagen, moet je op zoek naar de gulden snede in zijn of haar gezicht!
Jaap
met dank aan o.a. kennislink.
De gulden snede is een stukje eeuwenoude raadselachtige wiskunde. De gulden snede of ‘Divina Proportia’ (goddelijke proportie) kort men af met de Griekse letter Φ (spreek uit: ‘Fie’). Φ heeft niets met π te maken. π ken je wel van de wiskundeles. Het drukt de verhouding van de diameter van een cirkel uit in relatie tot de omtrek en heeft als waarde 3,14. Φ geeft een verhouding van lijnstukken aan – vandaar de Engelse naam: The Golden Ratio.
Sommige onderzoekers denken dat de beroemde piramides van de oude Egyptenaren zijn gebouwd op basis van het getal Φ.
De Griekse wijsgeer Euclides beschreef als eerste het getal Φ, maar men gebruikte de gulden snede waarschijnlijk al eerder. De oude Egyptenaren bouwden hun piramides op basis van de gulden snede. Ook in het Parthenon, een tempel ter ere van de godin van welvaart en vrede Athena, kun je Φ terugvinden. Φ is ook op andere plaatsen te ontdekken: bijvoorbeeld in de verhouding tussen de lengte van het middelste botje in je vinger tot het langste botje en het kortste botje. Ook in het hartslagpatroon – zichtbaar gemaakt op een ECG – is tussen de hartslagen de verhouding van Φ terug te vinden. In de vroege middeleeuwen bedacht Fibonacci het antwoord op de vraag waarom deze verhouding zo vaak terug te vinden is.
In 1202 publiceerde Leonardo Fibonacci een bijzondere rij getallen: elk getal van de rij (behalve de eerste twee) is gelijk aan de som van de twee voorgaande getallen. Dat levert de volgende rij getallen op: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, enzovoorts. De Fibonacci-reeks zit vol met eigenaardigheden, zoals elke optelsom van tien opeenvolgende getallen uit de reeks is deelbaar door elf (probeer maar eens). Om de zestig getallen herhaalt het laatste cijfer, bijvoorbeeld het tweede getal is 1, het tweeënzestigste getal in de reeks eindigt op een 1 (….4052739537881), het 122ste getal in de reeks eindigt op een ….. 1 (…..14028366653498915298923761), etcetera.
De Fibonacci-reeks vormt de rekenkundige basis voor de gulden snede. Dit is in 1611 ontdekt door de beroemde astronoom Johannes Kepler. Als je een getal uit de Fibannaci-reeks deelt door zijn voorganger uit de reeks, dan benadert de breuk het gulden-snede-getal Φ. In de tabel staan enkele getallen uit de Fibonacci-reeks gedeeld door het voorgaande getal, afgerond op vijf decimalen.
De Fibonnanci-reeks komt in de natuur op allerlei onverwachte plaatsen voor. Als je bijvoorbeeld goed kijk naar de verdeling van de zonnebloemzaden in een zonnebloem, kun je spiralen zien waarvan sommige met de klok meedraaien en sommige tegen de klok in lopen. De grootte van de zonnebloem bepaalt het aantal spiralen. Meestal tel je 34 spiralen die de ene kant op wijzen en (je raadt het al) 55 die de andere kant op wijzen. Bestudeer eens een bloemkool van de bovenkant. Als je goed kijkt, kun je hier ook een spiralenpatroon zien (meestal 5 met de klok mee en 8 tegen de klok in). Ook de rangschikking van blaadjes rond de stengel van een plant volgt vaak de beroemde reeks. De blaadjes zitten niet allemaal aan dezelfde kant van een stengel, maar staan spiraalsgewijs om de stengel. Het aantal blaadjes per omloop volgt de Fibonacci-reeks, bijvoorbeeld per omwenteling om de stam staan twee blaadjes (1/2) of acht blaadjes per drie omwentelingen.

Wonderlijke spiraal
Deze logaritmische spiraal komt in de natuur veelvuldig voor. Deze wonderlijke spiraal (Spiralis Mirabilis) wordt ook wel de Spiraal van Archimedes genoemd. Archimedes was helemaal gebiologeerd door spiralen en schreef er zelfs een compleet boek over.Veel slakkenhuizen zijn volgens dit patroon opgebouwd. Ook de hoorns van bijvoorbeeld een ram volgen dit patroon, maar ook sterrenstelsels. Uit figuur 5 blijkt dat de Spiralis Mirabilis rechtstreeks uit Φ is afgeleid. Kunstenaars maken veelvuldig van de spiraal gebruik. In de krullen van Leda, op het schilderij Leda en de zwaan van Leonardo da Vinci kun je ook de Spira mirabilis vinden.

Knappe vriendin
Waarom stemt het ene schilderij meer met de werkelijkheid overeen dan een ander schilderij? Volgens Pacioli (1445- 1517) – een Italiaanse wiskundige kloosterling – komt dat doordat de schilder de wetten van de wiskunde gehoorzaamt. Diepte in een schilderij, de verdeling van ruimtelijke vlakken over het linnen, liggen volgens Pacioli allemaal vast in wiskundige verhoudingen zoals Φ. Hij schreef drie boeken (bekend onder de naam ‘De Divina Proportione’) waarin hij de schilderkunst tot wiskundige figuren en vergelijkingen probeerde terug te brengen. Ook schilders uit recentere tijden zoals Mondriaan gebruikten bewust dan wel onbewust de gulden snede.
Niet alleen in de kunst kom je Φ tegen, ook menselijke schoonheid volgt de wetten van de gulden snede. In het menselijke gezicht vind je allerlei verhoudingen die de gulden snede benaderen. Bijvoorbeeld de verhouding van de lengte van je neus tot de breedte. Of de afstand tussen je ogen tot de totale breedte van je gezicht. Misschien verklaart het aantal gulden sneden die in het gezicht voorkomen, of iemand knap is of niet. Dus als je wilt weten of je een knappe vriend of vriendin aan de haak hebt geslagen, moet je op zoek naar de gulden snede in zijn of haar gezicht!

Jaap
met dank aan o.a. kennislink.