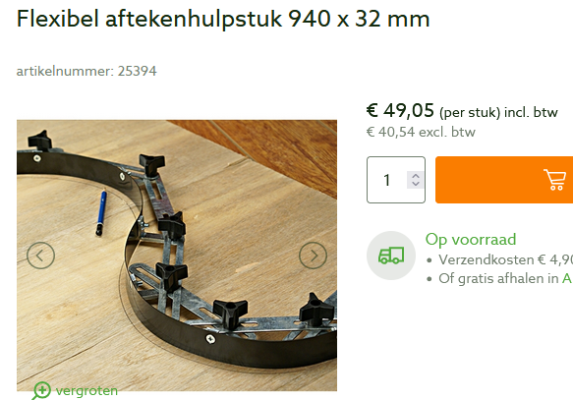
nu het kopiëren van de glooiing van de wang uitgezocht is
Even ter meerdere eer en glorie van mijn autistische zelf: met een cirkel als copieermal maak je geen exacte copie. Je maakt een verkleining a rato v.d. cirkelstraal (althans bij een binnenbocht – bij een buitenbocht is het net het omgekeerde).
Dit is niet intuitief: de afstand vh potlood tov de trapboom blijft toch gelijk? Zegge en schrijve de straal vd cirkel? Inderdaad. Daarom moet je het limietengrapje toepassen om het te zien. Dat jullie het limietengrapje niet kennen is perfect normaal: ik heb het namelijk net zelf verzonnen.
Het limietengrapje is een dogma dat dicteert dat je – zoals in de wiskunde – de limieten van een bewering moet opzoeken om de bewering te testen aan de praktijk.
Eerst test je de ene limiet: een rechte lijn. Nou, dan klopt de copie perfect, dus je ziet het nog steeds niet

.
Daarna neem je de andere limiet: de grootst mogelijke kromming, m.a.w. het te copieren object is even rond als de copieermal.
Neem nu bvb die CD van 15cm als copieermal. Copieer nu evenwel niet een trapboom (noch een rechte), maar copieer bvb een kookpot die amper groter is in doormeter dan de CD, stel 20cm, om de limiet zo goed mogelijk te benaderen. Je zal nu merken dat je “copie vd kookpot” helemaal geen copie vd kromming vd kookpot is, maar een pietlullig cirkeltje met diameter van 20-15=5cm. Je hebt de kookpot dus niet gecopieerd, je hebt ‘m verkleind. Op de echte limiet wordt de copie zelfs een singulier punt, maar dit ter zijde.
DAT GEZEGD ZIJNDE: bij de combinatie trapboom/CD ga je dit effect niet zien.
Maar mijn autistische zelf wilde het effect toch even delen. Het kan namelijk echt van belang zijn als je nu bijvoorbeeld die trapboom zou willen opdikken: dan zou je wel degelijk zien dat de copie niet perfect aansluit. Dit was trouwens een voorbeeld ter illustratie: ik zou begot ook niet weten waarom je de trapboom zou opdikken.