Voor degenen die er over denken om driehoekige vormen te draaien is dit wellicht handig voor de plaatsbepaling van de drie benodigde centerpunten, uitgaande van de hoeveelheid die je wilt afvlakken.
Gisteren en vandaag even bezig geweest om dit te conceptualiseren en een slimme vriend heeft e.e.a. uit ge-algebraat en inzichtelijk gemaakt. Met de dikgedrukte formule is de afstand van de centerpunten tov het middelpunt te bepalen.
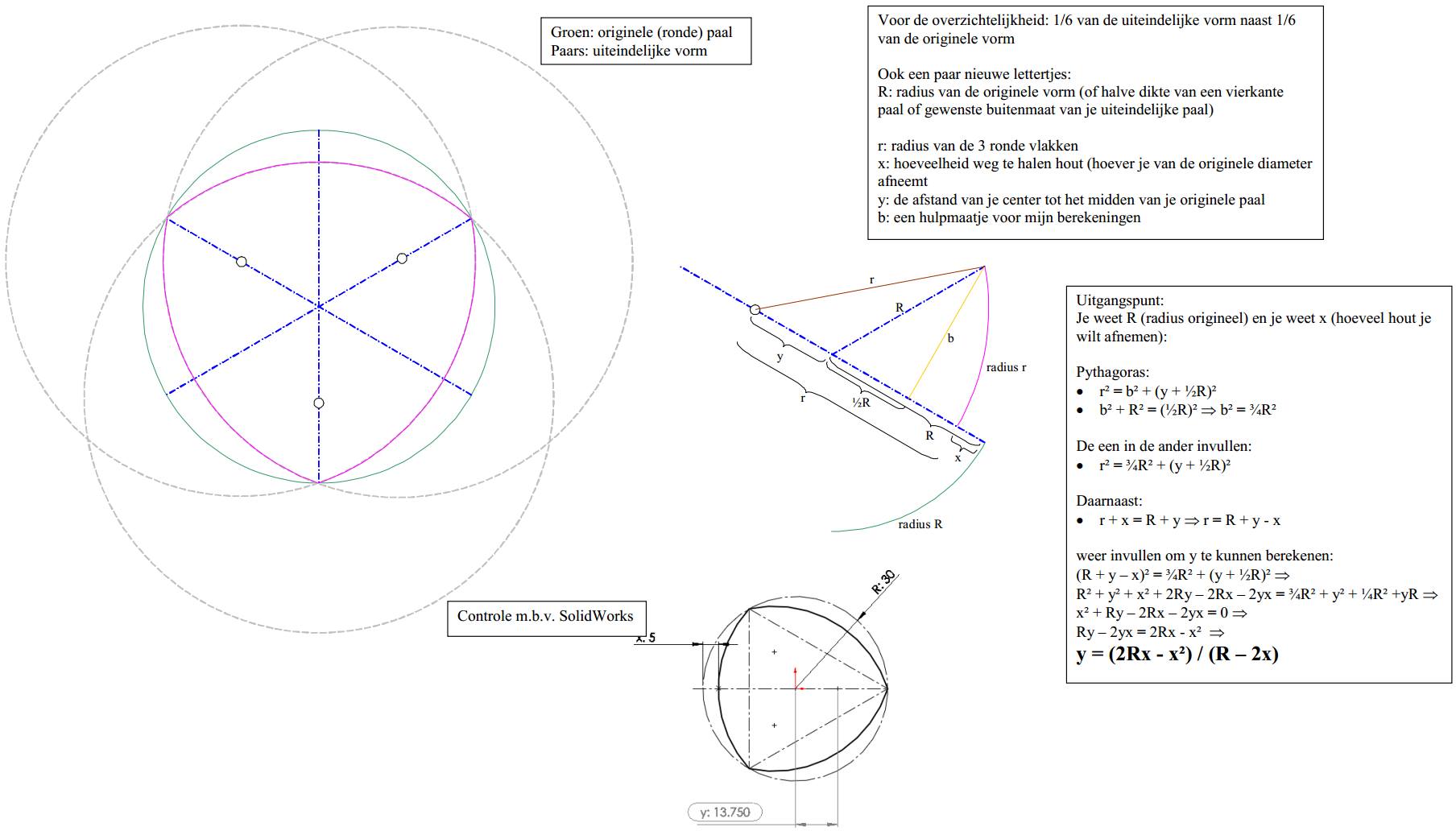
En hier is een manier om e.e.a. te construeren met een passer, gegeven een diameter van het dikste deel van de driehoek (VT) en de straal (RT) van de beschrijvende cirkel. Gaat wel uit van een middelpunt O in een rond object, is minder materiaal efficiënt. Is makkelijk op te lossen door punt O door het midden van driehoek PQR te laten lopen.
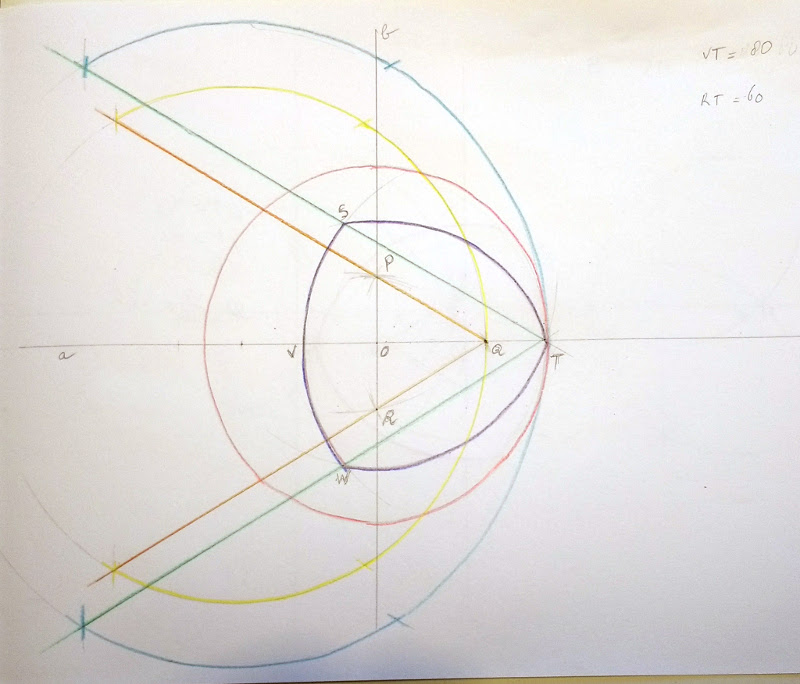
Uitleg van de constructie
1. Begin met een (horizontale) lijn a.
2. Teken daarop een afstand VT af (in dit geval 80mm) .
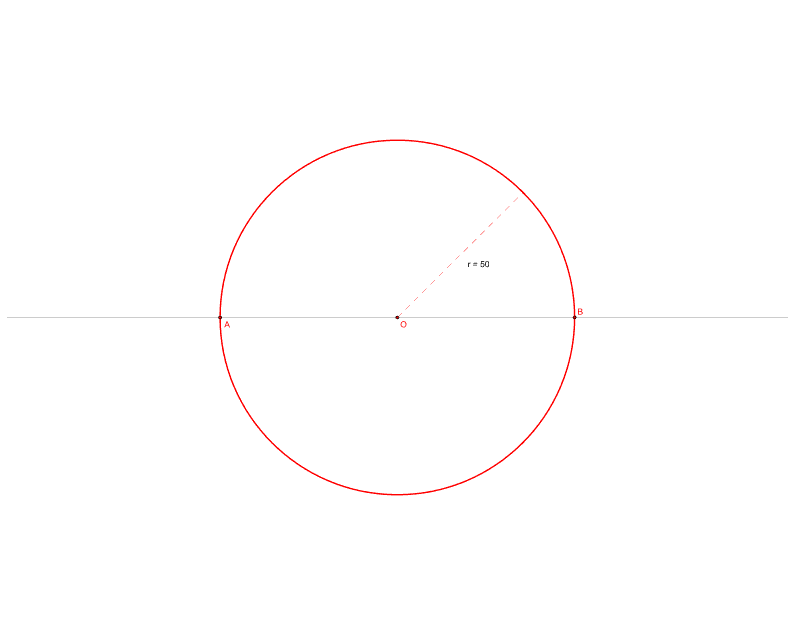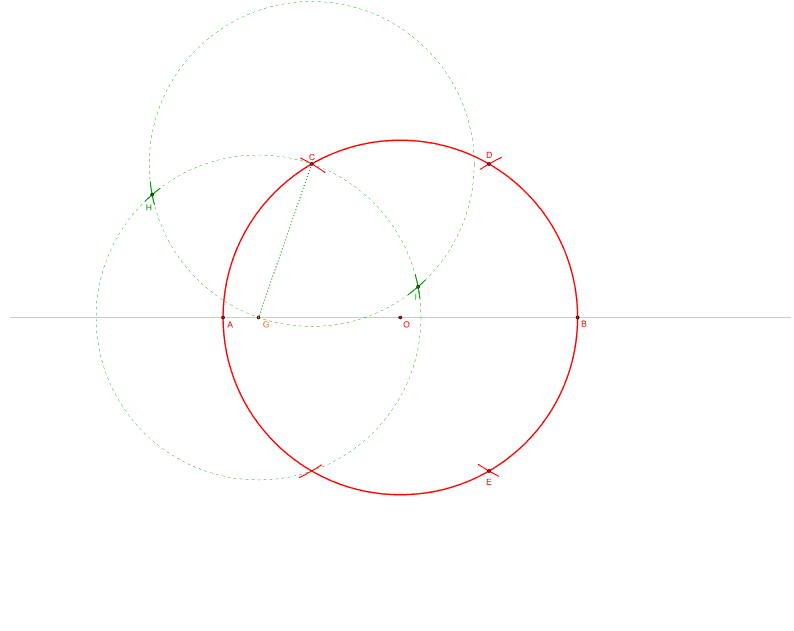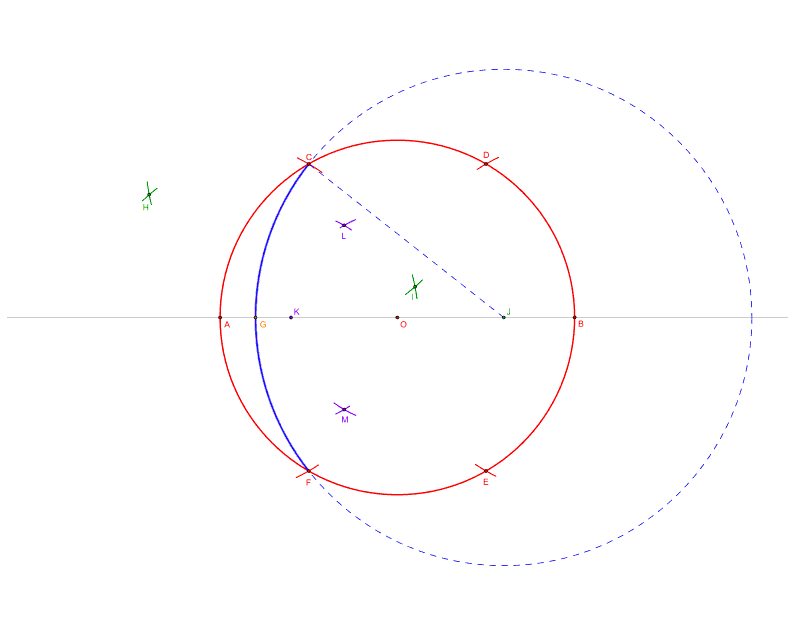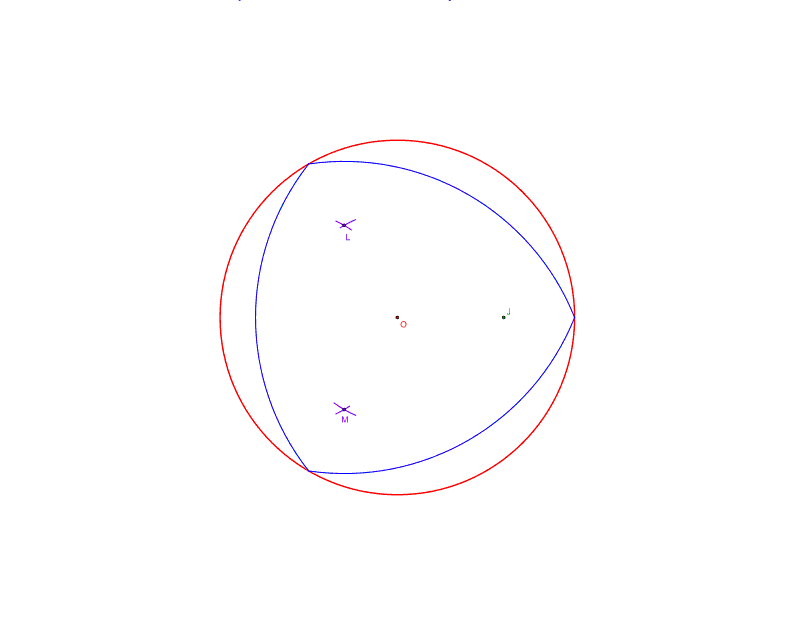
3. Teken een willekeurige cirkel met een middenpunt op lijn a, die door T loopt. (blauw)
4. construeer een gelijkzijdige driehoek (groen): met de de passer nog op de radius van de cirkel beginnen in punt T, streepje zetten waar de passer de blauwe cirkel raakt. vanuit dat punt nog een keer hetzelfde. Dit aan zowel de onder als de bovenzijde doen.
5. Zet de straal van de driehoek (VQ) uit: 60mm in dit geval. ( = gelijk aan RT en QS)
6. Maak een cirkel vanuit punt Q door V (paars). Deze snijdt de groene driehoek in S en W.
7. Op punt Q truukje 4 herhalen (gele cirkel en oranje driehoek)
8. Stel de passer weer in op lengte VQ (60mm)
9. Teken vanuit punt T een cirkel. Deze snijdt de oranje driehoek in P en R
10. Teken vanuit punt P een cirkel deze snijdt de groene driehoek én de paarse lijn SW in W
11. Teken vanuit punt R een cirkel deze snijdt de groene driehoek én de paarse lijn ST in W
12. Niet noodzakelijk; trek een lijn b door punten P en Q. Deze snijdt lijn a in punt O. Dit is het middelpunt van de cirkel die precies de driehoek raakt in T (rood)
Eerste probeersel waarmee het balletje aan het rollen kwam

Gisteren en vandaag even bezig geweest om dit te conceptualiseren en een slimme vriend heeft e.e.a. uit ge-algebraat en inzichtelijk gemaakt. Met de dikgedrukte formule is de afstand van de centerpunten tov het middelpunt te bepalen.

En hier is een manier om e.e.a. te construeren met een passer, gegeven een diameter van het dikste deel van de driehoek (VT) en de straal (RT) van de beschrijvende cirkel. Gaat wel uit van een middelpunt O in een rond object, is minder materiaal efficiënt. Is makkelijk op te lossen door punt O door het midden van driehoek PQR te laten lopen.

Uitleg van de constructie
1. Begin met een (horizontale) lijn a.
2. Teken daarop een afstand VT af (in dit geval 80mm) .
3. Teken een willekeurige cirkel met een middenpunt op lijn a, die door T loopt. (blauw)
4. construeer een gelijkzijdige driehoek (groen): met de de passer nog op de radius van de cirkel beginnen in punt T, streepje zetten waar de passer de blauwe cirkel raakt. vanuit dat punt nog een keer hetzelfde. Dit aan zowel de onder als de bovenzijde doen.
5. Zet de straal van de driehoek (VQ) uit: 60mm in dit geval. ( = gelijk aan RT en QS)
6. Maak een cirkel vanuit punt Q door V (paars). Deze snijdt de groene driehoek in S en W.
7. Op punt Q truukje 4 herhalen (gele cirkel en oranje driehoek)
8. Stel de passer weer in op lengte VQ (60mm)
9. Teken vanuit punt T een cirkel. Deze snijdt de oranje driehoek in P en R
10. Teken vanuit punt P een cirkel deze snijdt de groene driehoek én de paarse lijn SW in W
11. Teken vanuit punt R een cirkel deze snijdt de groene driehoek én de paarse lijn ST in W
12. Niet noodzakelijk; trek een lijn b door punten P en Q. Deze snijdt lijn a in punt O. Dit is het middelpunt van de cirkel die precies de driehoek raakt in T (rood)
Eerste probeersel waarmee het balletje aan het rollen kwam